Mechanical Vibrations and Fluid Structure Interaction

Theoretical and experimental non-linear vibrations of thin rectangular plates and curved panels subjected to out-of-plane harmonic excitation are investigated. Experiments have been performed on isotropic and laminated sandwich plates and panels with supported and free boundary conditions. A sophisticated measuring technique has been developed to characterize the non-linear behavior experimentally by using a Laser Doppler Vibrometer and a stepped-sine testing procedure. The theoretical approach is based on Donnell's non-linear shell theory (since the tested plates are very thin) but retaining in-plane inertia, taking into account the effect of geometric imperfections. A unified energy approach has been utilized to obtain the discretized non-linear equations of motion by using the linear natural modes of vibration. Moreover, a pseudo arc-length continuation and collocation scheme has been used to obtain the periodic solutions and perform bifurcation analysis. Comparisons between numerical simulations and the experiments show good qualitative and quantitative agreement. It is found that, in order to simulate large-amplitude vibrations, a damping value much larger than the linear modal damping should be considered. This indicates a very large and non-linear increase of damping with the increase of the excitation and vibration amplitude for plates and curved panels with different shape, boundary conditions and materials.

The nonlinear vibrations of a water-filled circular cylindrical shell subjected to radial harmonic excitation in the spectral neighbourhood of the lowest resonances are investigated experimentally and numerically by using a seamless aluminium sample. The experimental boundary conditions are close to simply supported edges. The presence of exact one-to-one internal resonance, giving rise to a travelling wave response around the shell circumference and non-stationary vibrations, is experimentally observed and the nonlinear response is numerically reproduced. The traveling wave is measured by means of state-of-the-art laser Doppler vibrometers applied to multiple points on the structure simultaneously. Chaos is detected in the frequency region where the travelling wave response is present. The reduced-order model is based on the Novozhilov nonlinear shell theory retaining in-plane inertia and the nonlinear equations of motion are numerically studied (i) by using a code based on arclength continuation method that allows bifurcation analysis in case of stationary vibrations, (ii) by a continuation code based on direct integration and Poincaré maps that evaluates also the maximum Lyapunov exponent in case of non-stationary vibrations. The comparison of experimental and numerical results is particularly satisfactory.

The large amplitude forced vibrations of thin rectangular plates made of different types of rubbers are investigated both experimentally and theoretically. The excitation is provided by a concentrated transversal harmonic load. Clamped boundary conditions at the edges are considered, while rotary inertia, geometric imperfections and shear deformation are neglected since they are negligible for the studied cases. The von Kármán nonlinear strain-displacement relationships are used in the theoretical study; the viscoelastic behaviour of the material is modelled using the Kelvin-Voigt model, which introduces nonlinear damping. An equivalent viscous damping model has also been created for comparison. In-plane pre-loads applied during the assembly of the plate to the frame are taken into account. In the experimental study, two rubber plates with different material and thicknesses have been considered; a silicone plate and a neoprene plate.

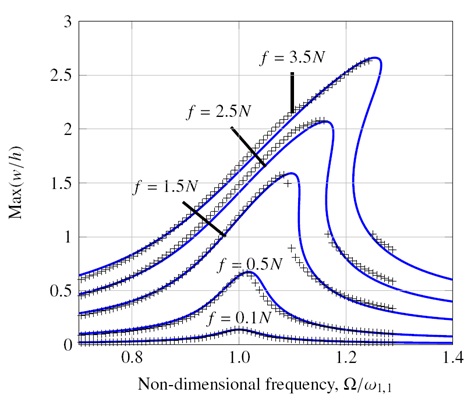
The plates have been fixed to a heavy rectangular metal frame with an initial stretching. The large amplitude vibrations of the plates in the spectral neighbourhood of the first resonance have been measured at various harmonic force levels. A laser Doppler vibrometer has been used to measure the plate response. Maximum vibration amplitude larger than three times the thickness of the plate has been achieved, corresponding to a hardening type nonlinear response. 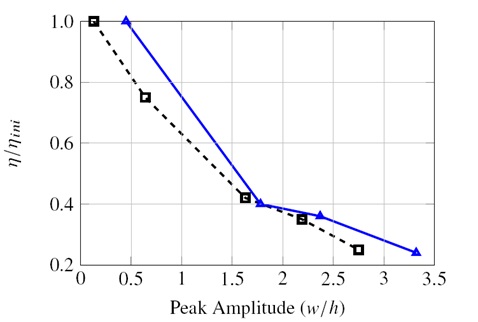Experimental frequency-response curves have been very satisfactorily compared to numerical results. Results show that the identified retardation time decreases when the excitation level is increased, whereas the equivalent viscous damping increases.